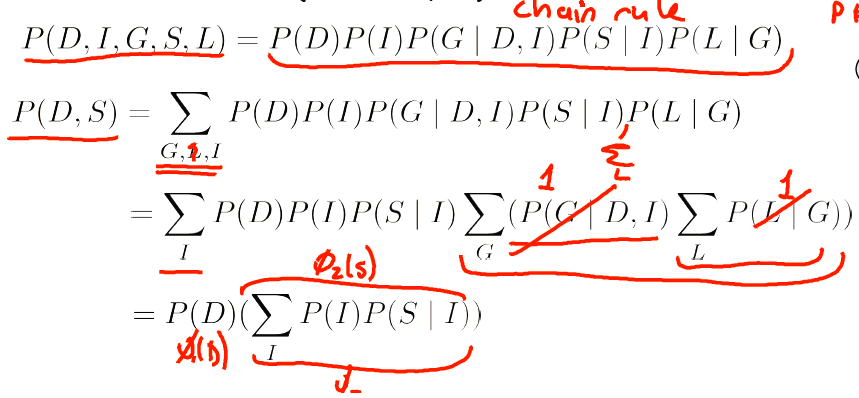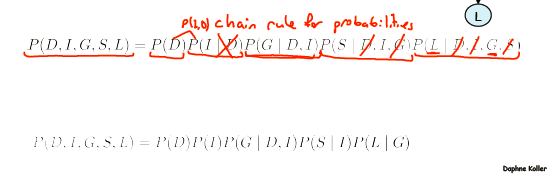之前忘记强调重要的差异:链式法则的条件概率和贝叶斯网络的链式法则之间的差异
条件概率链式法则
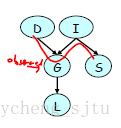
贝叶斯网络链式法则,如图1
图1
乍一看非常easy认为贝叶斯网络链式法则不就是大家曾经学的链式法则么,事实上不然,后面详述。
上一讲谈到了概率分布的因式分解
能够看到条件概率的独立性能够直接从概率分布表达式看出来。
我们已经用概率图模型把概率关系用图形化G表示了,独立性能从图上直接看出来吗?
当然。上一讲已经详解过了概率图中概率的流动关系.
当G已知时,S和D之间的概率才干相互影响。
以下定义一个依赖隔离的概念。
依赖隔离(D-separation)
在Z已知的情况下,X与Y之间没有通路。
则称之为X与Y依赖隔离。记作
介绍个定理:“图不通就独立定理”(当然是为了好理解)
这个定理是说。若概率图满足依赖隔离
则有X与Y条件独立
来证明一下,如今用的是贝叶斯网络链式法则。如图2
图2
利用的还是之前那个把求和拆分的Trick。这里要注意一開始求和的脚标是G、I、L
如今分给了3部分L和G部分求和后当然就等于了1,可是I部分则不然,被求和的部分是S,而求和脚标是I,这样就没法继续合并了。
只是我们回忆之前的独立等价条件最后一条是说:
这样就搞定了。发现D与S还是独立的。这样就证明了“图不通就独立定理”。
那么不禁要问,图什么情况下不通呢?
先说结论:在已知父节点时,该节点与后代节点以外的节点不通。
姑且叫做“不通原则”
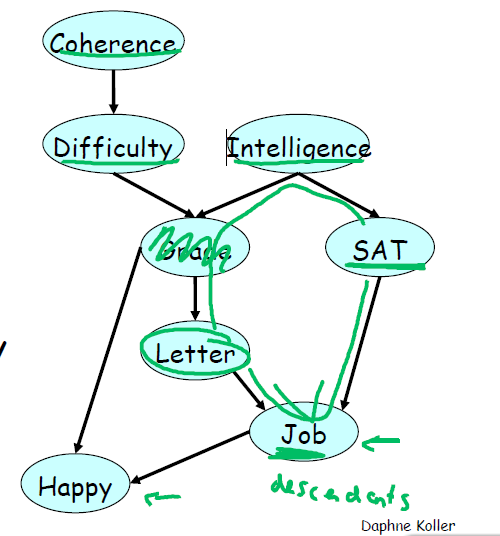
说的好啰嗦,直接看图,如图3
图3
我们以Letter节点作为样例。他的父节点时Grade,他的子孙是Job和Happy,所以他和剩下来的SAT、Intelligence、Difficulty、Coherence不通了。
粗略分析下,这个环上面走不通是由于Grade已知了;以下走不通是由于Job不知道。分析原理上一讲已经详述了。
定义一个Imap
既然图不通就独立,假设这个不通的图G相应的概率分布是P,我们就称G是P的I-map(independencymap)。
假设独立的概率分布P能够依照某个图G分解。那么G就是P的Imap。
反过来,假设G是概率分布P的Imap,那么P能够依照G来进行分解。
因此概率图的就有了2种等价的观点
1.概率图G是用来表示概率分布P的。
2.P是用来表达概率图G所展示的独立关系的。
证明一下概率图和概率分布为啥是一回事
先写出图1中的条件,如图4所看到的,用条件概率的链式法则写出P,由G中连接关系能够化简成为贝叶斯网络的链式法则。
图4
尤其注意为什么有
这里要用到之前说明的“不通原则”。L在已知D、G、I、S的前提下,他的非后代节点(他也没有后代节点)是D、I、S,所以直接去掉。
这就说明了概率独立关系与概率图的连接关系事实上是一回事。
以下介绍朴素贝叶斯模型
这个朴素贝叶斯叫做(Naïve Bayes)又叫(IdiotBayes…)
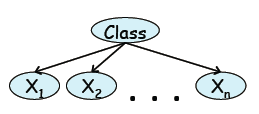
主要的朴素贝叶斯模型如图5。
图5
全部的X都是条件独立的,即
由贝叶斯网络的链式法则easy得到
有2类经常使用的朴素贝叶斯模型
举个样例说明两种贝叶斯模型各自是怎么起作用的。如今有一篇文档,由非常多单词组成。如今有2个类别可供选择各自是“有关財务”和“有关宠物”。如今要把这篇文章归档。
其一:伯努利朴素贝叶斯(Bernoulli Naive Bayes)
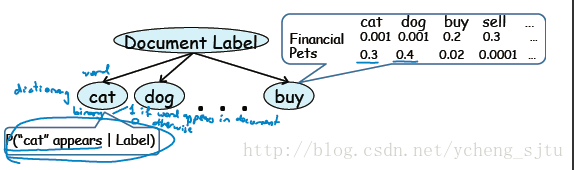
伯努利朴素贝叶斯如图6。
图6
这样的方式实质上是“查字典”。它把cat、dog、buy这些当做字典里的词目。
之所以伯努利是由于。这样的方式仅仅管分析文章里面有没有出现词典里的词目,而无论出现了多少次。词典的条目都是仅仅有0-1的二项分布随机变量。
文档属于这两类的概率分别为
每个小乘积项代表了“假设这是一篇財务文档,能出现cat字眼的概率是0.001”这种意义。
为啥这个朴素了,由于它如果了每一个词的条目出现是相互不影响的。
其二:多项式朴素贝叶斯(Multinomial Naïve Bayes)
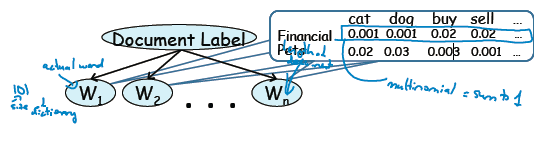
这样的方式与伯努利有本质不同,如图7
图7
W这些单元再也不是词典的条目了,而是待分类文章中的真实单词。
假如这篇文章写了1991个词,那么就有1991个W
文档属于这两类的概率依旧分别为
每个小乘积项代表了“假设这是一篇財务文档。在文章里随意一个位置出现cat的概率是0.001”这种意思。你看表还是那张表。可是如今全然不一样了。由于如今要求cat+dog+buy+sell这些概率加起来要等于1。而伯努利没这个限制,随意等于多少。这个差别非常重要。
为什么这个贝叶斯也是朴素的呢?由于它假定了在文章全部位置出现cat的概率是满足相同的分布的,实际明显不可能好不好。
就像“敬爱的”必定一般都会出如今开头。谁会在文章写到一半来句这个。。。
总之朴素贝叶斯确实朴素,它仅仅能用于随机变量相关性较弱的情况,但非常多情况实际确实挺弱的。。。所以朴素贝叶斯的效果Surprisingly effective
朴素贝叶斯被广泛使用于各种领域。这里就不展开了。长处还蛮多的。
欢迎參与讨论并关注和以及兴许内容继续更新哦~
转载请您尊重作者的劳动。完整保留上述文字以及文章链接,感谢您的支持!
版权声明:本文博主原创文章,博客,未经同意不得转载。